<< <i>Professor Sunnywood - Thank you for your time and effort with this post. I do have a question. Your explanation makes sense in the case of coherent light, however we are not viewing the coins under laser light. Natural light has no coherence, therefore the incident rays are of all phases. So how is it that cancellation can occur when incident and reflected rays have a random phase relationship? >>
This has already been addressed but I would like to add a bit to the answer. I posted something about the role coherence plays in thin film interference in a tone thread ATS last week that is worth expanding on here.
Every source of light has a level of coherence. Natural light is not perfectly incoherent and laser light is not perfectly coherent. It is most correct to speak of coherence time which is the amount of time the light is coherent before it changes to a different phase. As light is typically generated from an electron state transition at the molecular level the coherence of the light is related to the amount of time it takes to make this transition and emit the photon. For lasers there are other considerations since the state transitions are stimulated in a special way that creates coherence times much longer. Coherence is easier to think about in terms of length and the coherence time is easily converted into a length knowing the speed of light (which is of course different in different media, rising to the quantity known as the index of refraction).
Natural sunlight has a coherence length of around 400 nm which is plenty long to allow first order interference to occur. Most artificial light sources have a longer coherence length and can stay coherent in films thick enough that the natural color and absorption of the film override the thin film effect. I have noticed on some of my coins that the colors seem more washed out when I view them in bright sunlight but look much more vibrant when viewed under artificial light.
While Sunnywood did not reveal anything not already known in this thread, this is the first time I have seen all of this tied together into a neat package, which I think was excellent work.
Just came across this post. Wow! Very thought provoking material, Sunnywood! And Barberian's point is well taken, too…
One point to briefly consider are the differences in color refraction created by not so much by the specific material of the coin, but the actual refractory angle of the coin itself, which, of course, can be created by the minting procedures themselves. I’m thinking specifically between the differences in refraction between a coin that has been minted in a brilliant fashion as opposed to a coin which has been created by matte or sandblast methods, thereby ‘roughing’ the metal surface, and creating a million tiny little refractory angles, or, in effect, ‘mirrors’. Conversely, one may look at the ‘brilliant’ surface as ‘one’ singular mirror. Irrespective of the thickness of the toning layer of the material, the basic surface texture will remain static.
So if we look at the metal surface from this perspective, it stands to reason that any given metal surface (be that surface copper, nickel, silver or gold) should refract light at different angles depending on whether the surface is completely flat (like that created on a brilliant proof surface, with, theoretically, one consistant refractory angle – at least on the macro level) or the surface which comprises multiple tiny refractory variable degree angles, such as those that may be created by the process of minting a ‘textured’ matte proof surface.
So with the former, the angle of incidence will be much different (less?) in the volume of air and the toning layer. In the latter, the angle of incidence should be greater, as the actual surface area of the ‘matte’ surface is greater (albeit from having multiple refractory angles), and the refractory bending of light will therefore be greater, and in theory create the need to turn the refracting surface to an angle by which the ultimate refractory index is greatest. So in collector’s terms, this would account as an explanation as to why a brilliant proof coin will typically reflect color at many angles while rotated, while a matte proof coin will necessarily require the holder of the coin to rotate the coin in an axial manner to find the ultimate refractory angle, or ultimate color of the coin.
This has been my basic understanding of the light refracted by various surfaces - Would you agree with this observation?
I have seen some old PCI American Silver Eagles selling on ebay recently. The have 100% white on the slab but are target toned. Does PCGS cross these or do they consider them AT?
Comments
<< <i>Professor Sunnywood - Thank you for your time and effort with this post. I do have a question. Your explanation makes sense in the case of coherent light, however we are not viewing the coins under laser light. Natural light has no coherence, therefore the incident rays are of all phases. So how is it that cancellation can occur when incident and reflected rays have a random phase relationship? >>
This has already been addressed but I would like to add a bit to the answer. I posted something about the role coherence plays in thin film interference in a tone thread ATS last week that is worth expanding on here.
Every source of light has a level of coherence. Natural light is not perfectly incoherent and laser light is not perfectly coherent. It is most correct to speak of coherence time which is the amount of time the light is coherent before it changes to a different phase. As light is typically generated from an electron state transition at the molecular level the coherence of the light is related to the amount of time it takes to make this transition and emit the photon. For lasers there are other considerations since the state transitions are stimulated in a special way that creates coherence times much longer. Coherence is easier to think about in terms of length and the coherence time is easily converted into a length knowing the speed of light (which is of course different in different media, rising to the quantity known as the index of refraction).
Natural sunlight has a coherence length of around 400 nm which is plenty long to allow first order interference to occur. Most artificial light sources have a longer coherence length and can stay coherent in films thick enough that the natural color and absorption of the film override the thin film effect. I have noticed on some of my coins that the colors seem more washed out when I view them in bright sunlight but look much more vibrant when viewed under artificial light.
While Sunnywood did not reveal anything not already known in this thread, this is the first time I have seen all of this tied together into a neat package, which I think was excellent work.
One point to briefly consider are the differences in color refraction created by not so much by the specific material of the coin, but the actual refractory angle of the coin itself, which, of course, can be created by the minting procedures themselves. I’m thinking specifically between the differences in refraction between a coin that has been minted in a brilliant fashion as opposed to a coin which has been created by matte or sandblast methods, thereby ‘roughing’ the metal surface, and creating a million tiny little refractory angles, or, in effect, ‘mirrors’. Conversely, one may look at the ‘brilliant’ surface as ‘one’ singular mirror. Irrespective of the thickness of the toning layer of the material, the basic surface texture will remain static.
So if we look at the metal surface from this perspective, it stands to reason that any given metal surface (be that surface copper, nickel, silver or gold) should refract light at different angles depending on whether the surface is completely flat (like that created on a brilliant proof surface, with, theoretically, one consistant refractory angle – at least on the macro level) or the surface which comprises multiple tiny refractory variable degree angles, such as those that may be created by the process of minting a ‘textured’ matte proof surface.
So with the former, the angle of incidence will be much different (less?) in the volume of air and the toning layer. In the latter, the angle of incidence should be greater, as the actual surface area of the ‘matte’ surface is greater (albeit from having multiple refractory angles), and the refractory bending of light will therefore be greater, and in theory create the need to turn the refracting surface to an angle by which the ultimate refractory index is greatest. So in collector’s terms, this would account as an explanation as to why a brilliant proof coin will typically reflect color at many angles while rotated, while a matte proof coin will necessarily require the holder of the coin to rotate the coin in an axial manner to find the ultimate refractory angle, or ultimate color of the coin.
This has been my basic understanding of the light refracted by various surfaces - Would you agree with this observation?
Duane
WOW !!! That 81 s is the koolest Morgan ever...
Old thread alert. Sorry, selfishly bringing this up so I can easily find it for researching one of @Insider2’s quizzes.
Note: Refraction
A great old thread and a pleasure to read again... A lot of good information here. Cheers, RickO
i sometimes see the Sunnywood progression on coins other than Morgans ...
My Coin Blog
My Toned Lincoln Registry Set
I use three references, one concise table and two coins: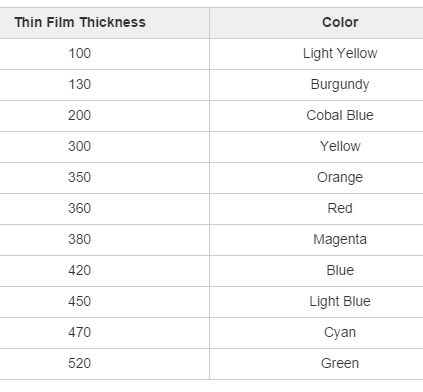


I personally like the bullseye pattern. My PCGS MS64 model:


Would you call this (Below) a, type of , "Bow Tie effect lamination" ?

.